Isomap (Isometric Feature Mapping), không giống như PCA (tuyến tính), Isomap là một phương pháp giảm chiều phi tuyến tính.
Hình ảnh dưới đây, được lấy từ bài báo gốc của Tenenbaum và cộng sự, minh họa cách Isomap hoạt động.

Ở phần A, chúng ta thấy rằng hai điểm gần nhau trong Không gian Euclide trong tập dữ liệu Swiss roll này có thể không phản ánh sự giống nhau nội tại giữa hai điểm này.
Trong B, một đồ thị được xây dựng với mỗi điểm là n hàng xóm gần nhất (ở đây là K = 7). Khoảng cách địa lý ngắn nhất sau đó được tính toán bằng thuật toán tìm đường như Đường ngắn nhất của Djikstra.
Trong C, đây là đồ thị 2D được khôi phục từ việc áp dụng MDS cổ điển (Multidimensional scaling) cho ma trận khoảng cách đồ thị. Một đường thẳng đã được áp dụng để biểu thị một cách gần đúng hơn và đơn giản hơn cho con đường thực sự được thể hiện trong A.
Isomap nên được sử dụng khi có ánh xạ phi tuyến tính giữa dữ liệu chiều cao hơn và đa tạp chiều thấp hơn của bạn (ví dụ: dữ liệu trên hình cầu).
Isomap tốt hơn các phương pháp tuyến tính khi xử lý hầu hết các loại theo dõi chuyển động và hình ảnh thực và bây giờ chúng ta sẽ xem xét ví dụ đã được sử dụng trong Tenenbaum et al. ảnh của các khuôn mặt ở các tư thế và điều kiện ánh sáng khác nhau.

Cách sử dụng isomap trong python
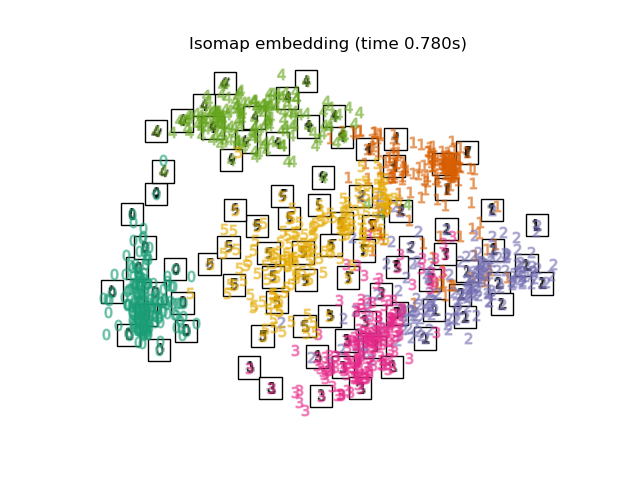
from sklearn.datasets import load_digits
from sklearn.manifold import Isomap
X, _ = load_digits(return_X_y=True)
embedding = Isomap(n_components=2)
X_transformed = embedding.fit_transform(X[:100])