Còn được gọi là phương trình động vật ăn thịt-con mồi, mô tả sự biến đổi trong quần thể của hai loài tương tác thông qua động vật ăn thịt. Ví dụ, cáo (động vật ăn thịt) và thỏ (con mồi). Đây là một mô hình cổ điển để đại diện cho sự năng động của hai quần thể.
Mô hình được đề xuất độc lập bởi Alfred J. Lotka vào năm 1925 và Vito Volterra vào năm 1926, và có thể được mô tả bởi:
[math]
\frac{du}{dt} = au - buv \\
\frac{dv}{dt} = -cv + dbu*v
[/math]
Trong đó:
- u: số lượng mồi (ví dụ: thỏ)
- v: số lượng động vật ăn thịt (ví dụ, cáo)
- a, b, c, d là các tham số không đổi xác định hành vi của quần thể:
- a là tốc độ phát triển tự nhiên của thỏ, khi không có cáo
- b là tỷ lệ chết tự nhiên của thỏ do bị ăn thịt
- c là tỷ lệ chết tự nhiên của cáo, khi không có thỏ
- d là yếu tố mô tả có bao nhiêu con thỏ bị bắt để tạo ra một con cáo mới
Chúng ta sẽ sử dụng X = [u, v] để mô tả trạng thái của cả hai quần thể.
Định nghĩa các phương trình:
import numpy as np
import pylab as p
# Definition of parameters
a = 1.
b = 0.1
c = 1.5
d = 0.75
def dX_dt(X, t=0):
""" Return the growth rate of fox and rabbit populations. """
return np.array([ a*X[0] - b*X[0]*X[1] ,
-c*X[1] + d*b*X[0]*X[1] ])
Cân bằng dân số
Trước khi sử dụng SciPy để tích hợp hệ thống này, chúng ta sẽ có một cái nhìn sâu hơn về trạng thái cân bằng. Trạng thái cân bằng xảy ra khi tốc độ tăng trưởng bằng 0. Điều này cho chúng ta điều kiện sau:
X_f0 = np.array([ 0. , 0.])
X_f1 = np.array([ c/(d*b), a/b])
np.all(dX_dt(X_f0) == np.zeros(2) ) and np.all(dX_dt(X_f1) == np.zeros(2)) # => True
Tính ổn định của các điểm cố định
Gần hai điểm này, hệ thống có thể được tuyến tính hóa: dX_dt = A_f * X trong đó A là ma trận Jacobian được đánh giá tại điểm tương ứng. Chúng ta phải xác định ma trận Jacobian
def d2X_dt2(X, t=0):
""" Return the Jacobian matrix evaluated in X. """
return np.array([[a -b*X[1], -b*X[0] ],
[b*d*X[1] , -c +b*d*X[0]] ])
Vì vậy, gần X_f0, đại diện cho sự tuyệt chủng của cả hai loài, chúng ta có:
A_f0 = d2X_dt2(X_f0) # >>> array([[ 1. , -0. ],
# [ 0. , -1.5]])
Gần X_f0, số lượng thỏ tăng lên và số lượng cáo giảm. Nguồn gốc do đó là một điểm yên ngựa.
Gần X_f1, chúng ta có:
A_f1 = d2X_dt2(X_f1) # >>> array([[ 0. , -2. ],
# [ 0.75, 0. ]])
# whose eigenvalues are +/- sqrt(c*a).j:
lambda1, lambda2 = np.linalg.eigvals(A_f1) # >>> (1.22474j, -1.22474j)
# They are imaginary numbers. The fox and rabbit populations are periodic as follows from further
# analysis. Their period is given by:
T_f1 = 2*pi/abs(lambda1) # >>> 5.130199
Tích hợp ODE bằng scipy.integrate
Bây giờ chúng ta sẽ sử dụng mô-đun scipy.integrate để tích hợp ODE. Mô-đun này cung cấp một phương pháp có tên là odeint, rất dễ sử dụng để tích hợp ODE:
from scipy import integrate
t = linspace(0, 15, 1000) # time
X0 = array([10, 5]) # initials conditions: 10 rabbits and 5 foxes
X, infodict = integrate.odeint(dX_dt, X0, t, full_output=True)
infodict['message'] # >>> 'Integration successful.'
infodict là tùy chọn và bạn có thể bỏ qua đối sốfull_output nếu không muốn. Nhập "thông tin (odeint)" nếu bạn muốn biết thêm thông tin về đầu vào và đầu ra
Bây giờ chúng ta có thể sử dụng Matplotlib để vẽ biểu đồ sự tiến hóa của cả hai quần thể:
rabbits, foxes = X.T
f1 = p.figure()
p.plot(t, rabbits, 'r-', label='Rabbits')
p.plot(t, foxes , 'b-', label='Foxes')
p.grid()
p.legend(loc='best')
p.xlabel('time')
p.ylabel('population')
p.title('Evolution of fox and rabbit populations')
f1.savefig('rabbits_and_foxes_1.png')
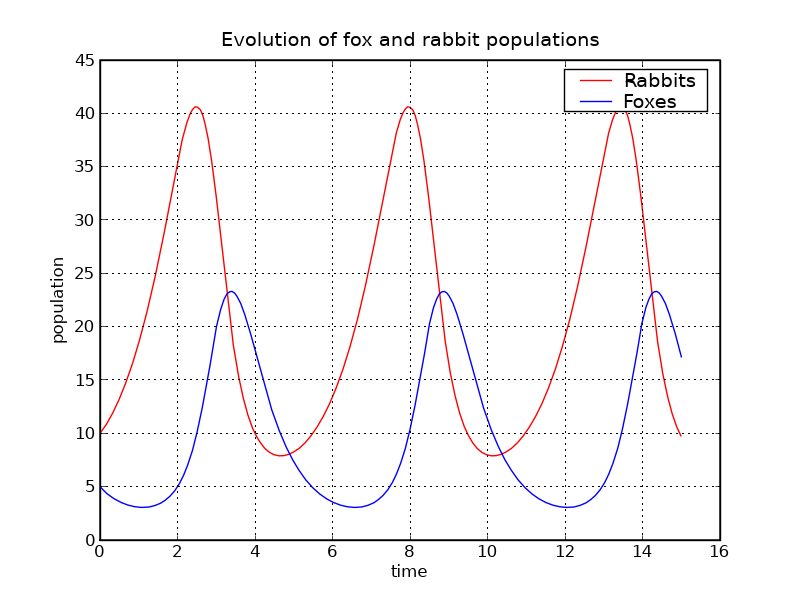
Các quần thể thực sự là tuần hoàn và chu kỳ của chúng gần với giá trị T_f1 mà chúng ta đã tính toán.