Phân phối T là gì?
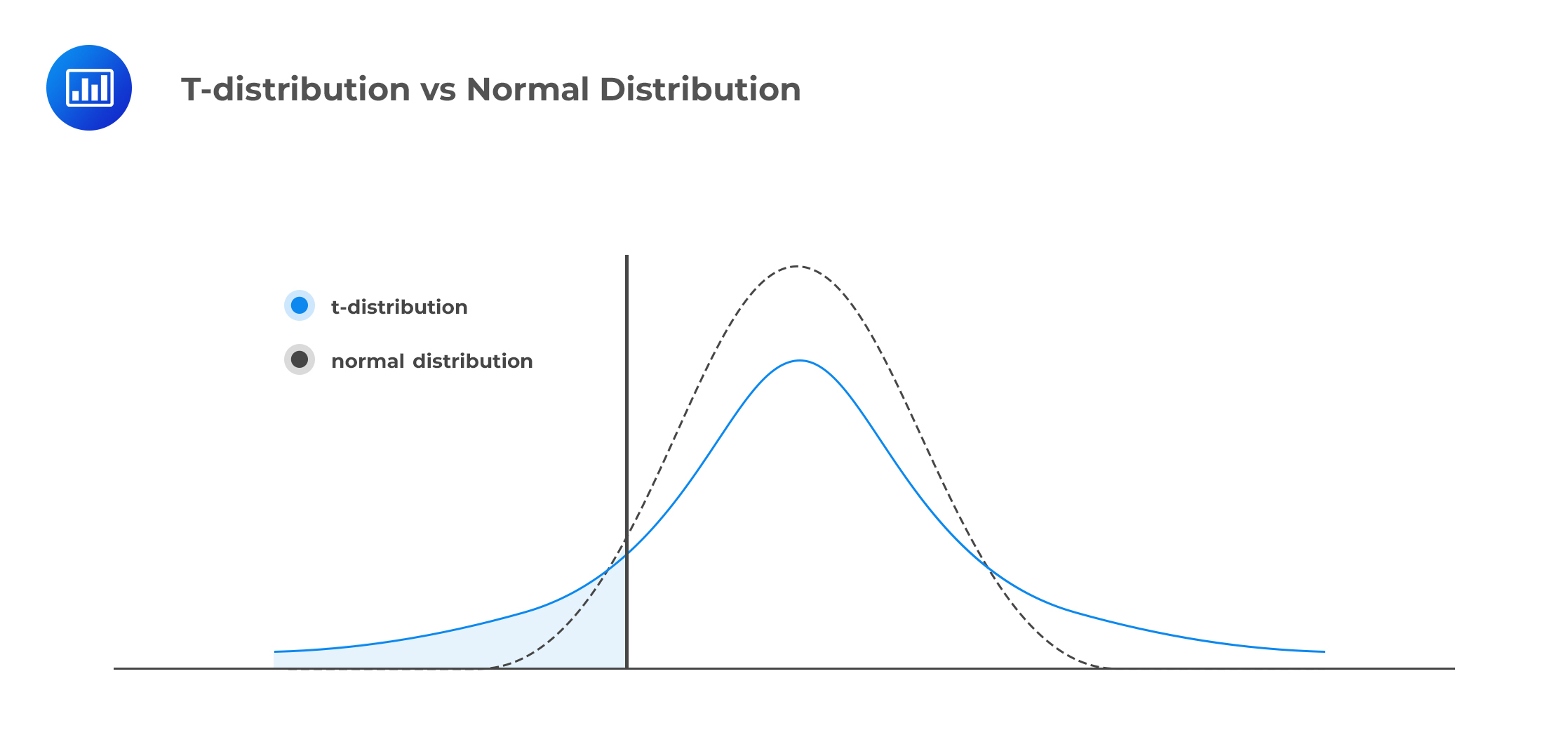
Phân phối T, còn được gọi là phân phối T Student, là một loại phân phối xác suất tương tự như phân phối chuẩn với hình chuông của nó nhưng có phần đuôi nặng hơn. Các phân phối T có xác xuất cho các giá trị cực trị lớn hơn so với các phân phối chuẩn, do đó có đuôi béo hơn.
Key note
- Phân phối T là phân phối xác suất liên tục của z-score khi độ lệch chuẩn ước tính được sử dụng ở mẫu số hơn là độ lệch chuẩn thực.
- Phân phối T, giống như phân phối chuẩn, có hình chuông và đối xứng, nhưng nó có đuôi nặng hơn, có nghĩa là nó có xu hướng tạo ra các giá trị khác xa giá trị trung bình của nó.
- Kiểm định T được sử dụng trong thống kê để ước tính mức độ quan trọng.
Phân phối T cho bạn biết điều gì?
Độ nặng của đuôi được xác định bởi một tham số của phân bố T được gọi là bậc tự do, với các giá trị nhỏ hơn cho đuôi nặng hơn và với các giá trị cao hơn làm cho phân phối T giống như một phân phối chuẩn với giá trị trung bình là 0 và độ lệch chuẩn là 1. Chỗ này nghĩa là bậc tự do càng nhỏ thì cái đuôi đồ thị nó càng (béo hơn, rộng hơn). Còn ngược lại thì nó gần giống với phân phối chuẩn

Khi một mẫu gồm
[imath]n[/imath]
quan sát được lấy từ normally distributed population (một quần thể phân bố chuẩn) có trung bình
[imath]M[/imath]
và độ lệch chuẩn
[imath]D[/imath]
, trung bình mẫu
[imath]m[/imath]
và độ lệch chuẩn mẫu
[imath]d[/imath]
, sẽ khác với
[imath]M[/imath]
và
[imath]D[/imath]
vì tính ngẫu nhiên của mẫu. (M và D viết hoa là của quần thể có phân bố chuẩn, còn m và d viết thường là của mẫu)
Theo định lý giới hạn trung tâm, phân phối lấy mẫu của một thống kê sẽ tuân theo phân phối chuẩn, miễn là kích thước mẫu đủ lớn. Do đó, khi chúng ta biết độ lệch chuẩn của tổng thể (tức biết D), chúng ta có thể tính z-score và sử dụng phân phối chuẩn để đánh giá xác suất với giá trị trung bình(M). Nhìn công thức tính z-score bên dưới
z-score
z-score (hay còn gọi là standard score) cho biết một phần tử có bao nhiêu độ lệch chuẩn so với giá trị trung bình.
Một z-score có thể được tính với độ lệch chuẩn tổng thể là:
[math]zscore = \frac{(x – M)}{D}[/math]
.
-
[imath]x[/imath]
là giá trị của phần tử mà chúng ta cần tính
-
[imath]M[/imath]
là trung bình quần thể (population mean)
-
[imath]D[/imath]
là độ lệch chuẩn của quần thể (population standard deviation)
Và giá trị này có phân phối chuẩn với giá trị trung bình 0 và độ lệch chuẩn 1.
t-score
Nhưng kích thước mẫu đôi khi nhỏ, và thường chúng ta không biết độ lệch chuẩn của tổng thể (Không biết D). Khi một trong hai vấn đề này xảy ra, các nhà thống kê dựa vào phân phối của thống kê t (còn được gọi là t-score), có giá trị được cho bởi:
[math] tscore = \frac{(m-M)}{ \frac{d}{\sqrt{n}} }[/math]
-
[imath]m[/imath]
là trung bình mẫu (sample mean)
-
[imath]M[/imath]
là trung bình quần thể (population mean)
-
[imath]d[/imath]
là độ lệch chuẩn của mẫu (standard deviation of the sample)
-
[imath]n[/imath]
là kích thước mẫu (sample size)
- Lưu ý chúng ta không biết
[imath]D[/imath]
trong trường hợp này
sự khác biệt giữa
[imath]d[/imath]
và
[imath]D[/imath]
làm cho phân phối trở thành phân phối T với
[imath](n - 1)[/imath]
bậc tự do hơn là phân phối chuẩn với trung bình 0 và độ lệch chuẩn 1.
Phân phối T (T distribution) cho phép chúng ta tiến hành phân tích thống kê trên một số tập dữ liệu không thích hợp để phân tích.
Bài tập áp dụng T Distribution
Công ty Cổ phần Acme sản xuất bóng đèn. Giám đốc điều hành tuyên bố rằng một bóng đèn Acme trung bình có tuổi thọ 300 ngày. Một nhà nghiên cứu chọn ngẫu nhiên 15 bóng đèn để thử nghiệm. Các bóng đèn được lấy mẫu có tuổi thọ trung bình là 290 ngày, với độ lệch chuẩn là 50 ngày. Nếu khẳng định của Giám đốc điều hành là đúng thì xác suất để 15 bóng đèn được chọn ngẫu nhiên có tuổi thọ trung bình không quá 290 ngày là bao nhiêu?
Đáp án
Điều đầu tiên chúng ta cần làm là tính toán thống kê T, dựa trên phương trình sau:
[math] tscore = \frac{(m-M)}{ \frac{d}{\sqrt{n}} }[/math]
Thay số ta có:
[math]
t = \frac{(290 - 300)}{ \frac{50}{\sqrt{15}} }
[/math]
[math]
t = \frac{-10}{12.909945} = - 0.7745966
[/math]
Tiếp theo chúng ta tính xác xuất tích luỹ (cumulative probabilities) ở đây mình tính bằng thư viện scipy của python luôn nhé:
Ta có bậc tự do
[math]
Df = 15 - 1 = 14
[/math]
from scipy.stats import t
print(t.cdf(-0.7745966, 14))
# 0.2257313120658352
kết quả: 0.2257313120658352
Máy tính hiển thị xác suất tích lũy: 0,226. Do đó, có 22,6% khả năng bóng đèn được lấy mẫu trung bình sẽ cháy hết trong vòng 290 ngày.
Tổng kết
Mình vừa hướng dẫn các bạn tính thống kê T và ứng dụng nó bằng python trong kiểm định thống kê. Hi vọng bài viết giúp bạn có cái nhìn và ứng dụng cụ thể của thống kê hơn. Đừng quên chia sẻ đăng ký tài khoản trên diễn đàn, join nhóm facebook, và đăng ký kênh youtube ủng hộ mình nhé